Mastering Binary Calculations and Conversions

Introduction

In the rapidly advancing world of technology, a profound understanding of binary calculations and conversions is paramount. Binary, a base-2 numeral system utilizing only two digits—0 and 1—forms the bedrock of digital information storage and processing in computers. This comprehensive guide will delve deeply into the intricacies of binary calculations and conversions, providing you with an extensive knowledge base encompassing this vital aspect of computing.

1. Understanding Binary Basics

Binary, as the name implies, is a base-2 numeral system. In stark contrast to the familiar base-10 (decimal) system, binary employs just two digits: 0 and 1. These two digits constitute the fundamental units of digital information representation and processing within computers. In essence, every piece of data, be it text, images, instructions, or raw data, is ultimately encapsulated and manipulated through the binary numeral system.

1.1 Binary Digits (Bits)

The smallest unit in binary, often referred to as a “bit,” embodies the essence of this system. A bit can take on one of two values: 0 or 1. However, binary’s true power lies in its scalability. By combining multiple bits, one can represent increasingly complex information. For instance, a group of 8 bits forms a “byte,” capable of encoding values spanning from 0 to 255. The synergy of these bits allows for the representation of a vast array of data, from simple alphanumeric characters to intricate graphics and multimedia.

1.2 Binary Counting

Counting in binary may initially seem alien compared to our everyday decimal system, but it follows a straightforward pattern. The primary distinction lies in the base and the available digits. While decimal counting relies on ten digits (0 through 9), binary utilizes only two (0 and 1). Let’s explore a quick comparison:

• Decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
• Binary: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010…

An intriguing observation emerges from this comparison. Binary numbers increase by powers of 2, mirroring the way decimal numbers ascend by powers of 10. This unique characteristic plays a pivotal role in binary calculations and conversions.

2. Binary Arithmetic

2.1 Addition in Binary

Binary addition, although analogous to its decimal counterpart, introduces distinct rules essential to binary arithmetic:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (with a carry-over of 1 to the next column)

To illustrate, consider the following binary addition:

   1101
+   101
-------
  10010

In this example, the binary numbers 1101 and 101 are added. Each column is treated individually, with carry-overs accurately considered. The result, 10010, highlights the fundamental principles of binary addition.

2.2 Subtraction in Binary

Binary subtraction aligns itself closely with the rules governing decimal subtraction. When subtracting 1 from 0, the binary system mandates borrowing 1 from the next column. Let’s examine an example:

   1101
-   101
-------
    100

In this scenario, 1101 is subtracted from 101, with careful consideration of borrowings. The outcome, 100, exemplifies binary subtraction’s mechanics.

3. Binary Conversions

3.1 Binary to Decimal

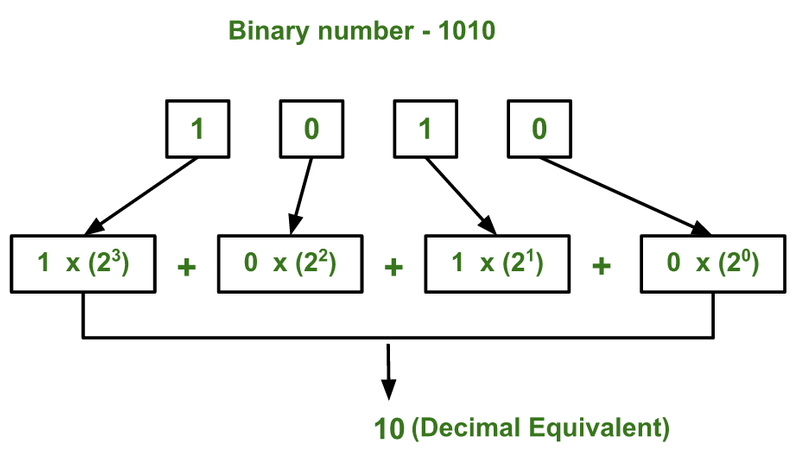
The conversion from binary to decimal is a fundamental operation involving the multiplication of each binary digit by the corresponding power of 2, with subsequent summation of the results. Commencing from the rightmost digit, commonly referred to as the least significant bit (LSB), and progressing leftward, each digit contributes to the final decimal value based on its position in the binary number. The powers of 2 associated with each digit increase by one with each step to the left.

To elucidate this process, let’s convert the binary number 1101 to its decimal counterpart:

(1 * 2^3) + (1 * 2^2) + (0 * 2^1) + (1 * 2^0) = 8 + 4 + 0 + 1 = 13 (in decimal)

This calculation demonstrates how each digit’s position is mapped to an appropriate power of 2, resulting in the decimal equivalent of 13.

3.2 Decimal to Binary

Converting a decimal number to binary entails a systematic approach of iteratively dividing the decimal value by 2 while keeping track of the remainders. These remainders, read from bottom to top, collectively construct the binary representation of the original decimal number.

To elucidate this process, let’s convert the decimal number 13 into its binary counterpart:

Decimal 13 ÷ 2 = Quotient 6, Remainder 1
Decimal 6 ÷ 2 = Quotient 3, Remainder 0
Decimal 3 ÷ 2 = Quotient 1, Remainder 1
Decimal 1 ÷ 2 = Quotient 0, Remainder 1

The process is repeated until the quotient reaches 0, with the remainders recorded in reverse order. Consequently, the binary representation of 13 is deduced as 1101.

4. Binary and Computers

Binary is not just a mathematical curiosity; it is the language of computers. In the digital realm, all data and instructions are communicated and processed in binary. Every text character, image pixel, and numerical value within a computer’s memory or storage is encoded as a series of binary digits.

In the heart of every computer, there is a central processing unit (CPU) that performs complex operations on binary data. These operations include arithmetic and logical calculations, data storage and retrieval, and control of various hardware components. The CPU interprets binary instructions fetched from memory, executes them, and produces binary results.

Understanding binary is, therefore, indispensable for programmers and computer scientists. When you write code in high-level programming languages like Python, Java, or C++, your instructions are eventually translated into binary code that the computer’s CPU can execute. Consequently, even if you primarily work with high-level languages, having a grasp of binary principles can enhance your ability to write efficient and optimized code.

5. Applications of Binary

Binary’s ubiquity extends far beyond computing and programming. It underpins various technological marvels, shaping the modern world in countless ways:

5.1 Digital Electronics

Binary is the lingua franca of digital electronics. From the microcontrollers in household appliances to the processors in smartphones, all digital devices communicate internally in binary. The binary system’s simplicity and efficiency make it the ideal choice for encoding and processing electronic signals.

5.2 Data Storage

The foundation of data storage devices, such as hard drives and solid-state drives, relies on binary. Data is stored as a sequence of binary digits, and these devices read and write data by manipulating binary information.

5.3 Networking and Communication

In the realm of networking

and communication, binary plays a pivotal role. Data transmission through cables, wireless signals, and the internet involves encoding information into binary form. This ensures reliable and efficient communication across vast distances.

5.4 Image and Audio Processing

Binary is instrumental in image and audio processing. Digital images are composed of pixels, each represented by binary values for color. Similarly, digital audio is sampled and encoded in binary format. Understanding binary is crucial for professionals working in graphic design, audio engineering, and multimedia production.

6. Advanced Binary Concepts

Beyond the fundamental principles of binary arithmetic and conversions, advanced binary concepts are essential for tackling complex computational problems. Here are some advanced topics:

6.1 Binary Fractions

While we’ve primarily discussed integers in binary, real-world applications often involve fractions. Binary fractions, like decimal fractions, can be represented using binary digits. This involves extending the principles of binary arithmetic to fractional parts.

6.2 Two’s Complement

Two’s complement is a vital concept for representing signed numbers in binary. It allows for the representation of both positive and negative integers in a consistent binary format and forms the basis for binary integer arithmetic in most computer systems.

6.3 Binary Operations

In computer science, binary operations encompass a wide range of algorithms and techniques for manipulating binary data. These operations include bitwise AND, OR, XOR, and bit shifting. They are used extensively in low-level programming, data compression, and encryption.

6.4 Binary Trees

Binary trees are fundamental data structures used in computer science for organizing and searching data efficiently. Understanding binary trees is crucial for software developers and computer scientists working on data-related problems.

7. Binary Errors and Error Detection

In the world of binary, errors can have significant consequences. A single flipped bit can corrupt data or cause software to malfunction. Error detection and correction techniques are vital in ensuring the reliability of digital systems. Concepts like parity checking and checksums play a crucial role in identifying and mitigating errors in binary data.

8. Binary Coding and Data Compression

Efficient binary coding and data compression are vital in optimizing data storage and transmission. Techniques like Huffman coding and Run-Length Encoding (RLE) are used to represent data more efficiently in binary form. Understanding these techniques is valuable for professionals working on data-intensive applications, such as multimedia streaming and data compression algorithms.

Conclusion

In conclusion, binary calculations and conversions are not mere theoretical concepts; they form the backbone of modern technology. From computer programming to digital electronics, binary is the language that enables the functioning of the digital world. A deep understanding of binary principles is invaluable for anyone working in technology-related fields, providing the keys to unlocking the vast potential of digital innovation. Whether you aspire to be a programmer, a hardware engineer, or simply wish to comprehend the inner workings of the digital universe, mastering binary is your gateway to a world of knowledge and limitless possibilities.